
This post “Monty Hall Solution” continues on from my previous post Monty Hall Problem – Can You Solve This Maths Puzzle? If you haven’t read that post, then read it now before reading this. Because I will now show you even more Monty Hall Solution coolness! We saw that you could increase (double) your chances of winning a car by understanding some maths, so let’s delve further into it and who knows, you might win something big (then again you might not, but hey!).
So what happens, if there are 4 doors instead of 3 doors? And what happens if there are 5 doors, 6 doors, hmmm, more code required – cool!
Checkout the code on GitHub.
Get my free Monty Hall Game on Google Play.
Does The Monty Hall Solution Hold True For 4 or More Doors?
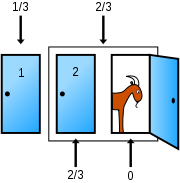
For 4 doors we would expect that the odds would be 1/4 (25%) for not changing Vs 1.5/4 (37.5%) for changing. “How did you get those figures?” I hear you ask. Well, with 4 doors, each door has a 25% chance of being correct. Our 1st chosen door has a 25% chance – the other 3 doors have a combined 75% chance. When Monty removes one of those 3 doors by opening it -the remaining 2 doors still have a combined 75% chance – which is now divided by the 2 remaining doors i.e. 37.50% chance each. Once again the figures from the 70 million simulations are very precise.
Doors in Game: 4 Unchanged Wins: 2498993, Changed Wins: 3750566 Unchanged Wins: 24.99%, Changed Wins: 37.51% Unchanged Wins: 2498720, Changed Wins: 3750419 Unchanged Wins: 24.99%, Changed Wins: 37.50% Unchanged Wins: 2500812, Changed Wins: 3748980 Unchanged Wins: 25.01%, Changed Wins: 37.49% Unchanged Wins: 2499171, Changed Wins: 3747829 Unchanged Wins: 24.99%, Changed Wins: 37.48% Unchanged Wins: 2499602, Changed Wins: 3749207 Unchanged Wins: 25.00%, Changed Wins: 37.49% Unchanged Wins: 2497548, Changed Wins: 3748332 Unchanged Wins: 24.98%, Changed Wins: 37.48% Unchanged Wins: 2499206, Changed Wins: 3749860 Unchanged Wins: 24.99%, Changed Wins: 37.50%
Monty Hall Solution with 5 Doors?
For 5 doors we would expect the odds to be 1/5 (20%) vs 1.33/5 (26.66%). These figures are derived as described above for 4 doors. So how does the simulation match up, well very precisely thank you:
Doors in Game: 5 Unchanged Wins: 1997315, Changed Wins: 2667064 Unchanged Wins: 19.97%, Changed Wins: 26.67% Unchanged Wins: 1999994, Changed Wins: 2666099 Unchanged Wins: 20.00%, Changed Wins: 26.66% Unchanged Wins: 2001180, Changed Wins: 2667386 Unchanged Wins: 20.01%, Changed Wins: 26.67% Unchanged Wins: 1999664, Changed Wins: 2667039 Unchanged Wins: 20.00%, Changed Wins: 26.67% Unchanged Wins: 2000629, Changed Wins: 2668808 Unchanged Wins: 20.01%, Changed Wins: 26.69% Unchanged Wins: 1999954, Changed Wins: 2665963 Unchanged Wins: 20.00%, Changed Wins: 26.66% Unchanged Wins: 1998652, Changed Wins: 2667357 Unchanged Wins: 19.99%, Changed Wins: 26.67%
Monty Hall Solution with 6 Doors?
Odds are 1/6 (16.66%) for not changing door, vs 1.25/6 (20.83%) for changing door. And yes, the simulation agrees…
Doors in Game: 6 Unchanged Wins: 1663952, Changed Wins: 2083233 Unchanged Wins: 16.64%, Changed Wins: 20.83% Unchanged Wins: 1667182, Changed Wins: 2083964 Unchanged Wins: 16.67%, Changed Wins: 20.84% Unchanged Wins: 1666971, Changed Wins: 2083919 Unchanged Wins: 16.67%, Changed Wins: 20.84% Unchanged Wins: 1666952, Changed Wins: 2083654 Unchanged Wins: 16.67%, Changed Wins: 20.84% Unchanged Wins: 1666734, Changed Wins: 2083798 Unchanged Wins: 16.67%, Changed Wins: 20.84% Unchanged Wins: 1666166, Changed Wins: 2082401 Unchanged Wins: 16.66%, Changed Wins: 20.82% Unchanged Wins: 1667218, Changed Wins: 2086789 Unchanged Wins: 16.67%, Changed Wins: 20.87%
And so on, as the number of doors increases we find that sticking or twisting becomes less important as 2 doors is an increasingly small fraction of the total number of doors i.e. 2/3, 2/4, 2/5, 2/6, 2/7 etc.
Monty Hall Solution with 3 – 9 Doors?
Just if you’re curious, here is a run of 10 million games for each number of doors (3-9), so a total of 70 million games. You can see the gap narrowing as the number of doors increases.
Doors in Game: 3 Unchanged Wins: 3332776, Changed Wins: 6667224 Unchanged Wins: 33.33%, Changed Wins: 66.67% Doors in Game: 4 Unchanged Wins: 2500354, Changed Wins: 3749370 Unchanged Wins: 25.00%, Changed Wins: 37.49% Doors in Game: 5 Unchanged Wins: 2000567, Changed Wins: 2665857 Unchanged Wins: 20.01%, Changed Wins: 26.66% Doors in Game: 6 Unchanged Wins: 1665930, Changed Wins: 2083850 Unchanged Wins: 16.66%, Changed Wins: 20.84% Doors in Game: 7 Unchanged Wins: 1430746, Changed Wins: 1713655 Unchanged Wins: 14.31%, Changed Wins: 17.14% Doors in Game: 8 Unchanged Wins: 1250934, Changed Wins: 1458256 Unchanged Wins: 12.51%, Changed Wins: 14.58% Doors in Game: 9 Unchanged Wins: 1111668, Changed Wins: 1271298 Unchanged Wins: 11.12%, Changed Wins: 12.71%
Feel free to download/fork the code and test it yourself, modify the number of doors and play around with it and see how the numbers come out. There is still something I want to do with this Monty Hall Problem / Monty Hall Solution before I put it down. Hmm, more thinking and typing required, expect a final post on this topic …
…And here it is, the final installment: Monty Hall Proof – The Formula
Questions or comments welcome below, and contributions to the code are welcome too, it is available on here Github 🙂
P.S. Nod to Cepheus~commonswiki for the images.

Have you added sound yet?