COVID-19 has changed a lot of things. All around the world Governments are restricting citizens movements to combat the spread of COVID-19 the deadly new Coronavirus. In Ireland the Government has restricted non-essential travel to a 2km zone around your place of residence. It turns out that’s an interesting choice, why so? Well we need to bring two things (circumference and area) together to find our answer. And then there’s a nice surprise at the end (unless you figure it out before you get there).
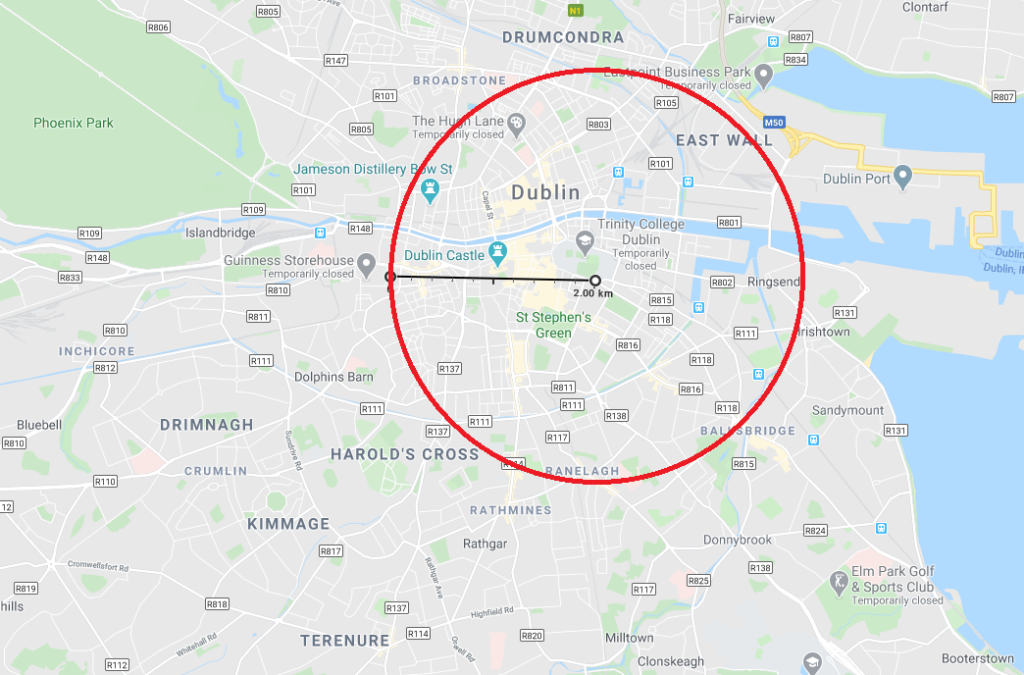
Circumference is king (Covid-19 is not)
Being confined to 2km can seem restrictive, but if you look at the image above it isn’t just 2km. So how far can you walk while keeping within the 2km limit? How much space is that? Think of your residence as the center of a circle with a radius of 2km, and you can go anywhere within that circle. The length of the red circle (circumference) above is given by twice the radius times Pi. What? Well let’s do it on the blackboard.
Blackboard #1
\( circumference = 2 * radius * \pi \)
We know the radius is 2km – as set by the Government:
\( circumference = 2 * 2 * \pi \)
\( circumference = 4 \pi \)
We know that \(\pi\) = 3.14
\( circumference = 4 * 3.14 = 12.6 km \)
So even with a mere 2km you can walk around a 12.6km circumference. And remember you have to walk 2km to get from the center (your residence) to the edge of the circle, and then another 2km to get back to the center afterwards. That gives a total of 16.6km, a lot more than a 2km limit might at first suggest.
Be careful though, the further you walk/run/cycle the greater the chance you’ll encounter COVID-19 #StayHomeStaySafe
Area is king (Covid-19 is not)
Walking around the edge of the circle (circumference) brings us from 2km to 12.6km (or 16.6km if you include getting to and from the circumference) which is a nice return. But what about the area within the circle, how much space do we actually have to move around in? Let’s illustrate the space we’re talking about with a super hi-tech graphic:
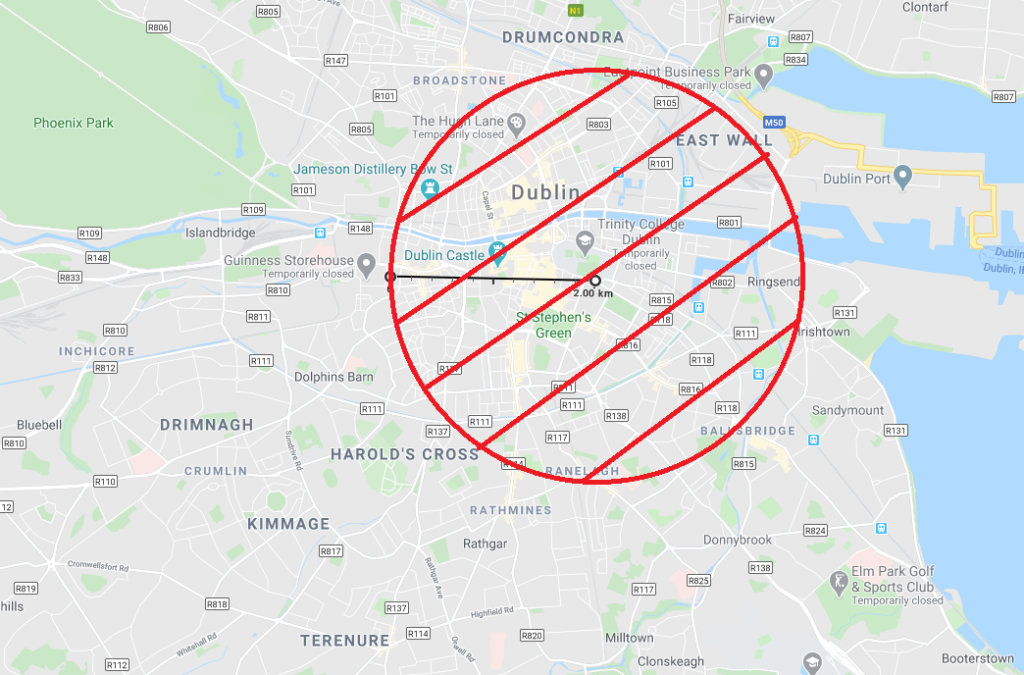
So how do we calculate the area of the circle in red above? Well \(\pi r^2\) will give us the area, where r is the radius = 2km.
Blackboard #2
\(area = \pi r^2\)
We substitute, r = 2
\(area = \pi * 2 ^ 2\)
\(area = 4\pi\)
We know that \(\pi\) = 3.14
\(area = 3.14 * 4\)
\(area = 12.6 km^2\)
Once again our 2km has given us a bigger number, this time an area of \(12.6km^2\). Did you notice anything about the circumference and the area? That’s right, they both have a magnitude of 12.6 (or \(4\pi\). INTERESTING. Yes, to a STEM NERD this is INTERESTING and necessitates more thinking, yum yum :7
Be careful though, the further you walk/run/cycle the greater the chance you’ll encounter COVID-19 #StayHomeStaySafe
Curiosity is king (Covid-19 is not)
Questions questions questions. Is this coincidence or consequence? What else, if anything, gives this same result where circumference equals area? Is there an infinite series of radius sizes, a finite set, or is this a unique situation? We can test these questions by using values other than 2km, we can try 3km, 4km, 4.5km etc. But then we’d have to try every possible number and that will take forever. So we can use algebra, yep yum yum algebra. After all, why test tons of numbers when you can just use one single letter, the letter ‘r’ in this case.
The trick here is to know that we are looking for the situation(s) where the circumference and the area will give us the same value (like the 12.6 we just saw above for r = 2). That means the magnitude of the circumference should equal the area. (Aside: Let’s leave the dimensions out for now and just deal with scalars, we’ll talk about the dimensions shortly). Ok. so let’s go back to the blackboard.
Blackboard #3
We want to find out when: circumference = area
\(2 \pi r = \pi r^2\)
We divide both sides by \(\pi\):
\(2r = r^2\)
We divide both sides by r:
\(2 = r\)
So we have a single answer. Only when r = 2 will we have the same value for circumference and area. And that is why 2km was an interesting choice. Do you reckon the Government knew this when they chose 2km? Probably not, but it’s interesting. Let’s have a look at values in the range 1 to 5 to see how they look.
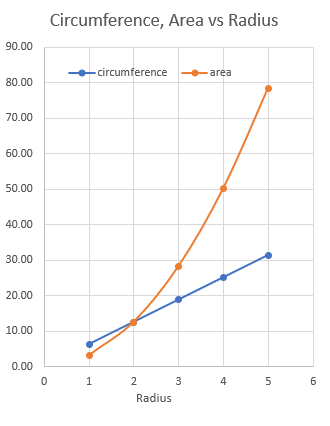
We can see the lines crossover over at radius = 2. As one would expect, since the circumference is linear while the area is quadratic, they continue to diverge as the radius increases.
There is more…
We should note the following minor points, before noting another major insight:
- The choice of unit (km, mile, furlong, light year) affects the magnitude. For example, if we convert to miles we’ll have 1.24miles (not 2km), and 1.24 is not the magic number in this case. In fact, we could pick arbitrary units of length to ensure we get 2, or we don’t get 2 as we wish.
- I have ignored the radius \(\leq\) 0 as they are not practical, but you can imagine the plot would be a projection through the y-axis. You will also note the plots intersect at r = 0, again this is not practically useful.
- You could get the equation of the line and the quadratic equation and verify their intersection points. I’ll leave that for your homework.
Be careful though, the further you walk/run/cycle the greater the chance you’ll encounter COVID-19 #StayHomeStaySafe
Did you notice the differential calculus?
I didn’t until it was pointed out by a Leaving Cert student (if there is a Leaving Cert this year). They noted that the circumference was the derivative of the area. Well spotted.
Blackboard #4
\(\pi r^2 = 2 \pi r\)
\(f'(\pi r^2) = 2 \pi r\)
This of course led to more questions. Is it particular to circles, or does it apply to triangles, squares, rectangles; does it apply to higher spatial dimension objects like spheres to circles, cubes to squares etc. They’re fun to think about and work out, or you can read more about these in the Further Reading section below, so you can grab your snorkel and go for a deep dive if you wish.
Further Reading:
- J. Tong, Area and perimeter, volume and surface area, College Math. J. 28 (1) (1997) 57
- M. Dorf & L. Hall, (2002) Solids in \(\rm I\!R ^n\) whose Area is the Derivative of the Volume
- Slideshow: Derivative relationships between volume and surface area of compact regions in \(\rm I\!R ^p \)
That’s All Folks
Thanks for reading, hope you enjoyed it. If you have any comments, or corrections feel free to leave a comment. Or you may like to read some of my other interesting blog posts involving maths.
Be careful though, the further you walk/run/cycle the greater the chance you’ll encounter COVID-19 #StayHomeStaySafe
